Say, A and B are libraries with 1000 books.
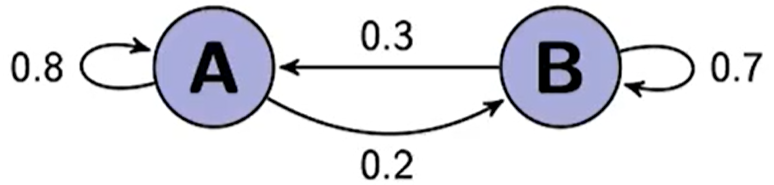
In the beginning, x0=[0.50.5]
Now, after 1 month, x1=[0.8⋅0.5+0.3⋅0.50.2⋅0.5+0.7⋅0.5]=[0.80.20.30.7][0.50.5]=Px1
P=[0.80.20.30.7]
Now, after 2 months, x2=Px1=P2x0
⋮
Now, after k months, xk=Pkx0
Steady State
Find the steady state of P=[0.80.20.30.7].
PqPq−qPq−Inq(P−In)q([0.80.20.30.7]−[1001])q[−0.20.20.3−0.3]q{−2x12x1+3x2−3x2=0=0{x1=3,x23+21[32]q=q=0=0=0=0=0=2}=q=[5352]
If a matrix is regular stochastic, it implies the existence of a steady state. (The converse is not necessarily true)
Convergence
We have x1,x2,x3,…xk. We want to know if while k→∞ xk will converge to a steady state.
If P is a regular stochastic matrix (vocabulary), then P has a unique steady-state vector q, and xk+1=Pxk converges to q as k→∞.
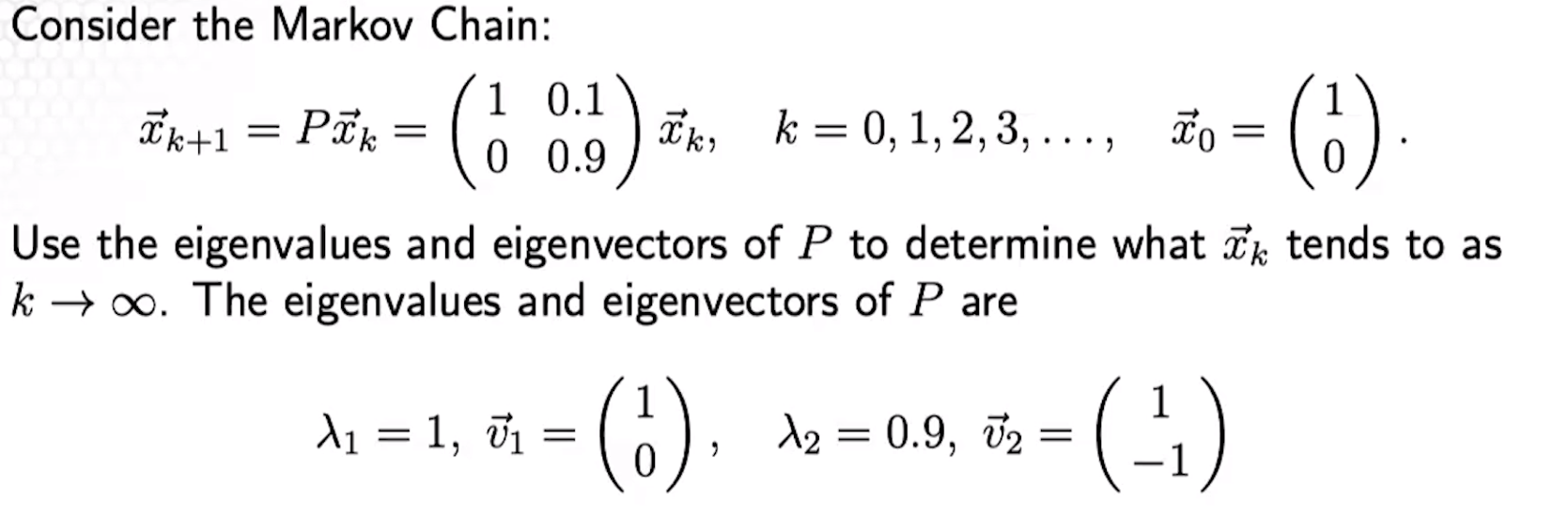 Say P has 2 eigenvalues (λ1 and λ2) and eigenvectors (v1 and v2).
Say P has 2 eigenvalues (λ1 and λ2) and eigenvectors (v1 and v2).
xk+1x0x1x1x1x2x1xk=Pxk=c1v1+c2v2=Px0=P(c1v1+c2v2)=c1λ1v1+c2λ2v2=Px1=P(c1λ1v1+c2λ2v2)=c1(λ1)kv1+c2(λ2)kv2=c1Pv1+c2Pv2=c1(λ1)2v1+c2(λ2)2v2
x0[10]c1=c1v1+c2v2=c1[10]+c2[1−1]=1c1=0
xk=v1

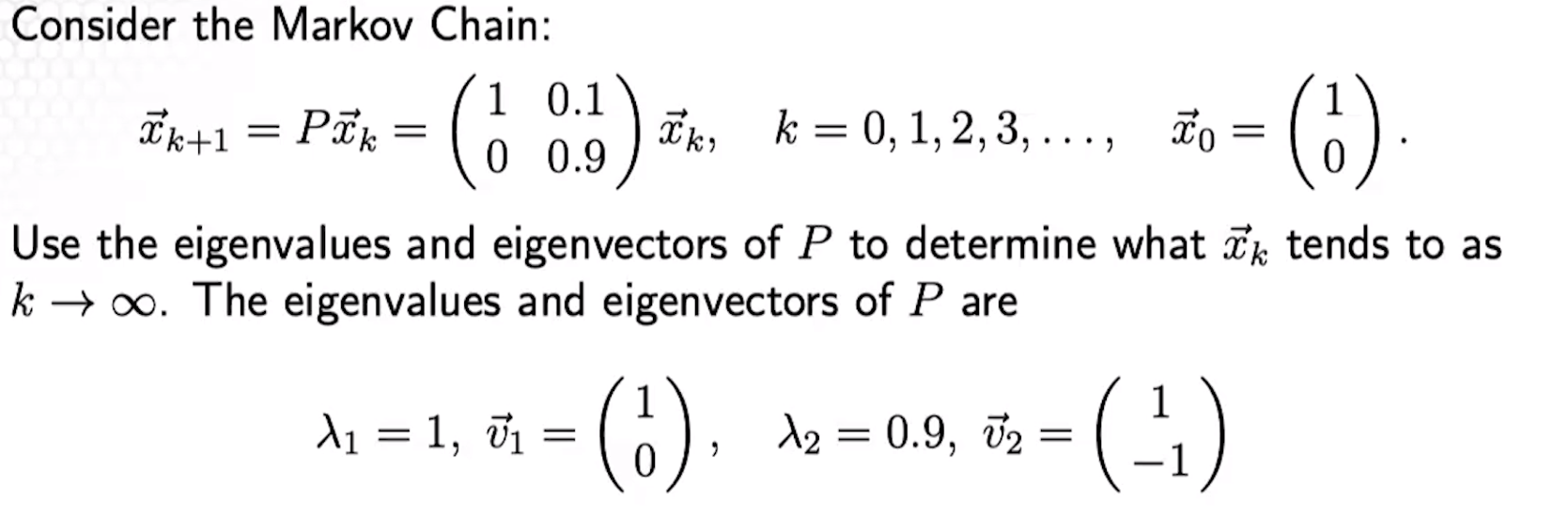 Say has 2 eigenvalues () and eigenvectors ().
Say has 2 eigenvalues () and eigenvectors ().