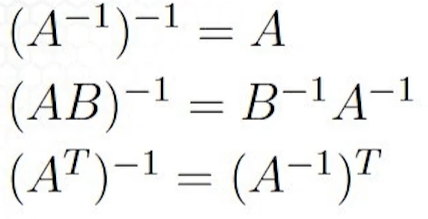Inverse of a Matrix

$A\in {\mathbb{R}}^{n\times n}$ is invertible if there is a $C\in {\mathbb{R}}^{n\times n}$ so that:

$AC=CA=I_n$ If so we write, $C=A^{-1}$

---

$A$ has an inverse if and only if there is a pivot on every row and column.

For a $2\times 2$

Compute

${\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]}^{-1}=\frac{1}{ad-bc}\left[\begin{array}{cc}d& -b\\ -c& a\end{array}\right]$

Use it to solve a Linear systems

$$\begin{array}{rl}A\vec{x}& =b\\ A^{-1}A\vec{x}& =A^{-1}b\\ I\vec{x}& =A^{-1}b\\ \vec{x}& =A^{-1}b\end{array}$$

Computing $A^{-1}$

1. Row reduce the augmented matrix $\left(A|I_n\right)$ to RREF.
2. If the reduction is in the form, $(I_n|B)$ then $A$ is invertible and $B=A^{-1}$. Else, $A$ is not invertible.

For example to find \left[ \begin{array} \\ 0 &1&2\\1&0&3\\0&0&1 \end{array} \right]^{-1}:

$$\begin{array}{rl}& =\left[\begin{array}{cccccc}0& 1& 2& 1& 0& 0\\ 1& 0& 3& 0& 1& 0\\ 0& 0& 1& 0& 0& 1\end{array}\right]\\ & =\left[\begin{array}{cccccc}1& 0& 0& 0& 1& -3\\ 0& 1& 0& 1& 0& -2\\ 0& 0& 1& 0& 0& 1\end{array}\right]\\ & =(I_3|A^{-1})\\ A^{-1}& =\left[\begin{array}{ccc}0& 1& -3\\ 1& 0& -2\\ 0& 0& 1\end{array}\right]\end{array}$$

Why does this work?

Using elementary matrices we can see that when we row reduce the augmented matrix $\left(A|I_n\right)$ to RREF, we are simple applying row operation, in other words we are simple applying transformations using elementary matrices. So if,

$$\begin{array}{rl}(E_k\cdots E_3{E}_2{E}_1)A& =I_n\\ E_k\cdots E_3{E}_2{E}_1& =A^{-1}\\ \text{as,}& \\ A^{-1}A& =I_n\end{array}$$

Properties