Leontif Input-Output Model

A Leontif Input-Output Model is a model that describes a economy whos’ parts need resources to provide resources.

$C$ is the consumption matrix. Entries of $C$ are $C_{i,j}$, with $C_{i,j}\in [0,1]$ , and $C\vec{x}=$ units consumed $\vec{x}-C\vec{x}=$ units left after internal consumption

$\vec{d}$ is the external demand. $\vec{x}$ is the produced quantity.

So for an economy we can derive the formula,

$\text{Total production}-\text{Total internal usage}=\text{Total external demand}$ $\vec{x}-C\vec{x}=\vec{d}$

Supposes we have a economy that looks like so, 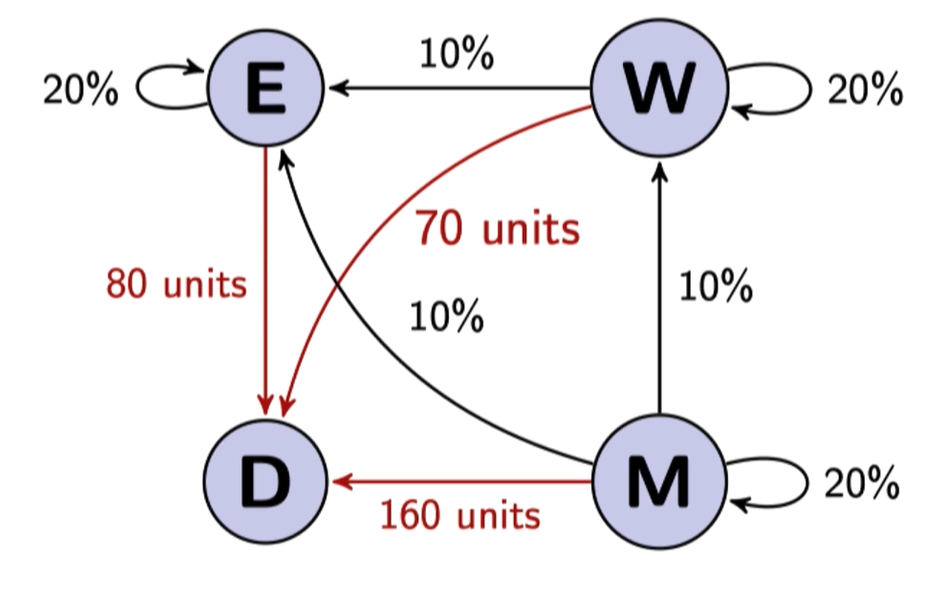E, W, M all produce something but D only consumes.

So we know that D is our$\text{ external demand}$ Our $\text{internal usage}$ usages are all the black arrows in the diagram. So we need to find $\text{total production}$

First define $\vec{x}=\left[\begin{array}{c}{x}_e\\ x_w\\ x_m\end{array}\right]$ We can construct $C\vec{x}$

\begin{align*} C\vec{x}&=x_e\begin{bmatrix} 20\% \\ 10\% \\ 10\% \end{bmatrix}+x_w\begin{bmatrix} 0\% \\ 20\% \\ 10\% \end{bmatrix}+x_m\begin{bmatrix} 0\% \\ 0\% \\ 20\% \end{bmatrix}\\ C\vec{x}&=x_e\begin{bmatrix} .2 \\ .1 \\ .1 \end{bmatrix}+x_w\begin{bmatrix} 0 \\ .2 \\ .1 \end{bmatrix}+x_m\begin{bmatrix} 0 \\ 0\\ .2 \end{bmatrix}\\ C&=\begin{bmatrix} .2 &0&0 \\ .1 &.2&0\\ .1 &.1&.2\end{bmatrix} \end{align*} }$$ We can construct $\textcolor{red}{\text{ external demand},\vec{d}.}$ $$\textcolor{red}{ \begin{bmatrix} 80 \\ 70 \\ 160 \end{bmatrix} }

Now we can put this in our formula to get $\vec{x}$

$$\begin{array}{rl}\vec{x}-C\vec{x}& =\vec{d}\\ (I-C)\vec{x}& =\vec{d}\\ \left(\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]-\left[\begin{array}{ccc}.2& 0& 0\\ .1& .2& 0\\ .1& .1& .2\end{array}\right]\right)\vec{x}& =\left[\begin{array}{c}80\\ 70\\ 160\end{array}\right]\\ \vec{x}& =\left[\begin{array}{c}100\\ 100\\ 225\end{array}\right]\end{array}$$