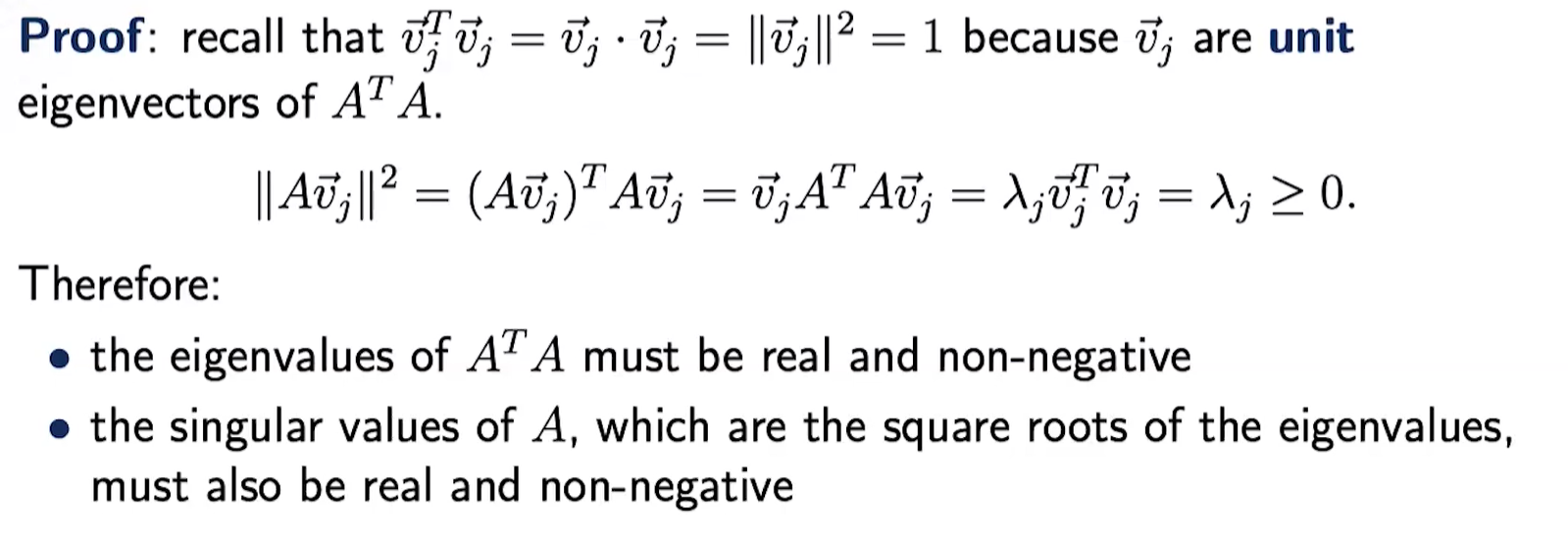Singular Values

The singular values of any $m\times n$ real matrix $A$ are the square roots of the eigenvalues of $A^{T}A$.

---

Say we want to find a $v$ that maximizes $||A\vec{v}||$ Where $||\vec{v}||=1$ This is the same thing as maximizing $||A\vec{v}|{|}^2$, so we have

$$\begin{array}{rl}||A\vec{v}|{|}^2& ={\vec{v}}^T{A}^{T}A\vec{v}\end{array}$$

$A^{T}A$ is always symmetric. After acknowledging that we can realizes that is a Constrained Optimization problem. $||\vec{v}||=1$ being the constraint. We will simply use the largest eigenvalue of $A^{T}A$ to find the largest value for $||A\vec{v}|{|}^2$. The location of this will simply be the corresponding normalized eigenvector.

The min value can be found using a similar method.

Calling singular values ${\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_n$ we can say that the ${\sigma }_1$ is the max value of $||A\vec{v}||$ and ${\sigma }_n$ is the min value.

Non-Negative Eigenvalues

The eigenvalues of $A^{T}A$ are non-negative.

Proof

From the above Proof we can see, $||A\vec{v}|{|}^2={\lambda }_i$ And hence, $||A\vec{v}||={\sigma }_i$