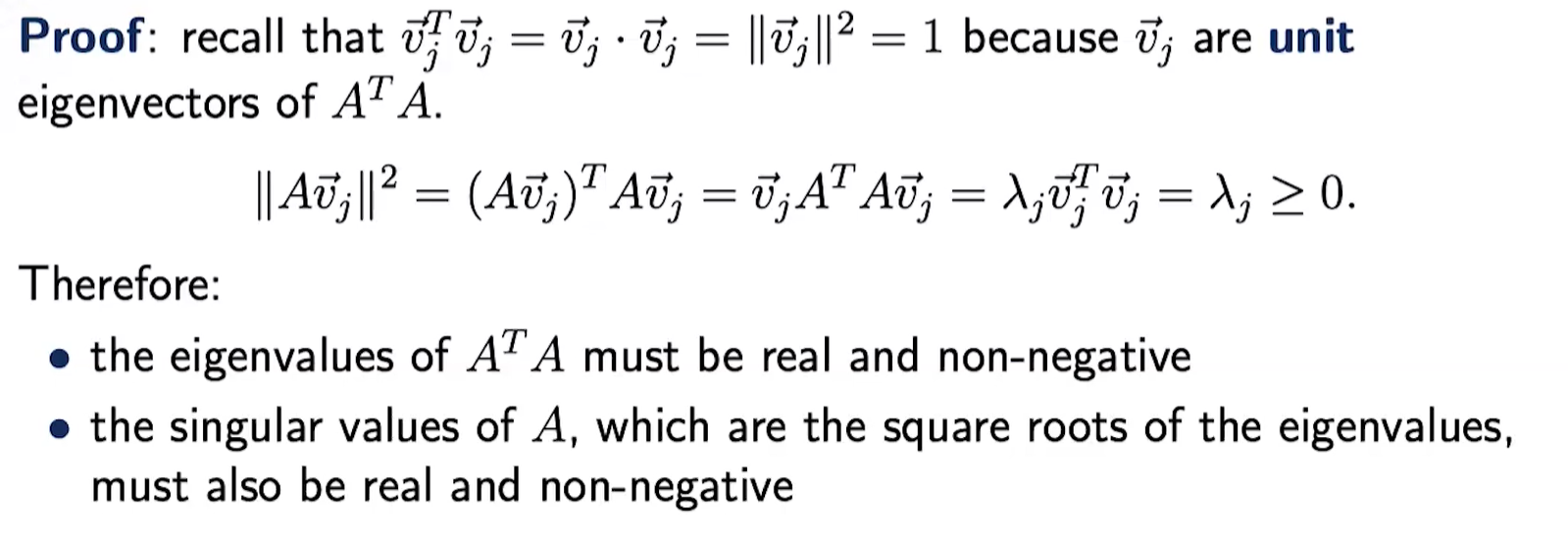Formulas

The Spectral Theorem

An $n\times n$ symmetric matrix $A$ has the following properties,

• All eigenvalues of $A$ are real.
• The eigenspaces are mutually orthogonal.
• $A$ can be diagonalized as $A=PD{P}^T$, where $D$ is diagonal and $P$ is orthogonal.

---

Non-Negative Eigenvalues

The eigenvalues of $A^{T}A$ are non-negative.

Proof

---