Singular Vectors

Theorem

Suppose ${\vec{v}}_i$ are the $n$ orthogonal eigenvectors of $A^{T}A$, ordered so that their corresponding eigenvalues satisfy ${\lambda }_1\ge {\lambda }_2\cdots \ge {\lambda }_n$. Suppose also that $A$ has $r$ non-zero singular values, $r\le n$. Then the set of vectors, $\{{\vec{v}}_{r+1},{\vec{v}}_{r+2},\dots ,{\vec{v}}_n\}$ is an orthogonal basis for $\text{Nul}A$, and the set $\{\overrightarrow{v_1},\overrightarrow{v_2},\dots ,\overrightarrow{v_r}\}$ is an orthogonal basis for $\text{Row}A$, and $\text{Rank}A=r$.

Proof

Using the same assumptions as above, it can be shown that, $\{A\overrightarrow{v_1},A\overrightarrow{v_2},\dots ,A\overrightarrow{v_r}\}$ or $\{\overrightarrow{u_1},\overrightarrow{u_2},\dots ,\overrightarrow{u_r}\}$ is an orthogonal basis for $\text{Col}A.$

Proof

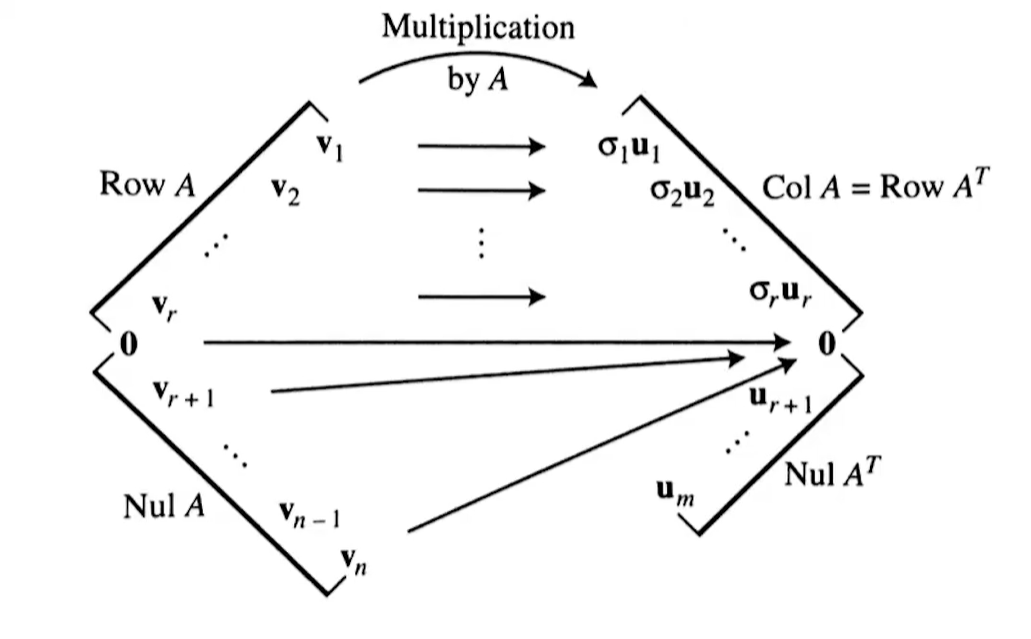
• Left Singular Vectors are the basis for $\text{Col}A$
• Right Singular Vectors are the eigenvectors of $A^{T}A$