Projections

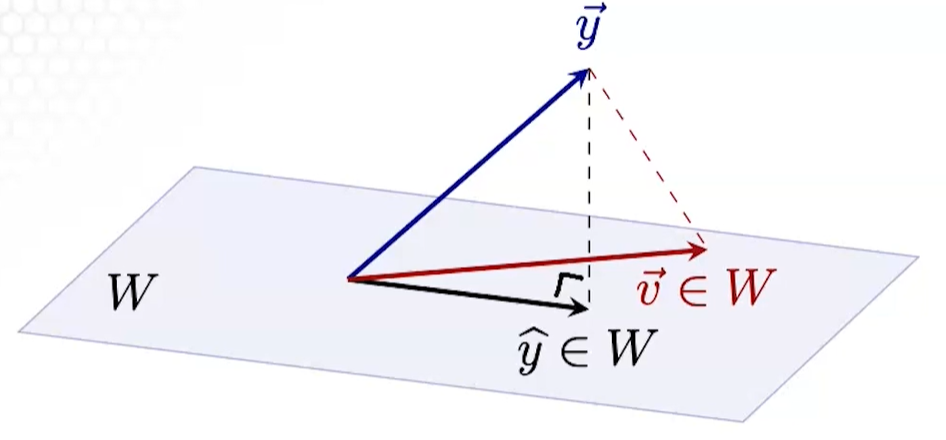
We have a subspace $W$ (the span of $\vec{u}$), and we want to find the vector ($\hat{y}$) closest to $\vec{y}$ in $W$. We also want to find $\vec{z}\in W^{\perp }$ such that $\vec{y}=\hat{y}+\vec{z}$. Diagrammatically, We know $\vec{z}\in W^{\perp }$, so: $\vec{z}\cdot \vec{u}=0$ We also know $\vec{y}=\hat{y}+\vec{z}$ and $\hat{y}=k\vec{u}$ ($k\in \mathbb{R}$), so:

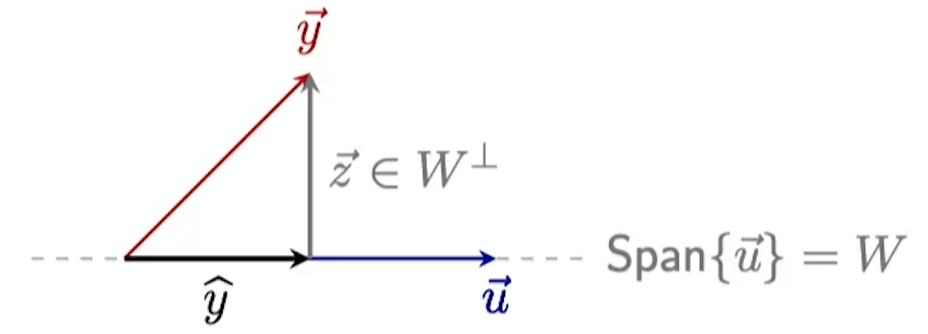$$\begin{array}{rlr}\vec{z}& =\vec{y}-k\vec{u}& \\ 0& =(\vec{y}-k\vec{u})\cdot \vec{u}& \\ & =\vec{y}\cdot \vec{u}-k\vec{u}\cdot \vec{u}& \\ k& =\frac{\vec{y}\cdot \vec{u}}{\vec{u}\cdot \vec{u}},& \vec{u}\ne \vec{0}\end{array}$$

So finally, $\hat{y}=\frac{\vec{y}\cdot \vec{u}}{\vec{u}\cdot \vec{u}}\vec{u}$

Orthogonal Projection

Let non-zero $\vec{u}\in {\mathbb{R}}^n$, and $\vec{y}\in {\mathbb{R}}^n$. The orthogonal projection of $\vec{y}$ onto $\vec{u}$ is the vector in the span of $\vec{u}$ that is closest to $\vec{y}$.

\text{proj}_\vec{u}\vec{y}=\frac{\vec{y}\cdot\vec{u}}{\vec{u} \cdot \vec{u}}\vec{u}

Also, $\vec{y}=\hat{y}+\vec{z}$ and, $\vec{z}\in W^{\perp }$

From this we can conclude (look at the diagram),

||\vec{y}||^2=||\text{proj}_\vec{u}\vec{y}||^2+||\vec{z}||^2

---

Best Approximation

Best Approximation Theorem

Let $W$ be a subspace of ${\mathbb{R}}^n,\vec{y}\in {\mathbb{R}}^n$, and $\hat{y}$ is the orthogonal projection of $\vec{y}$ onto $W$. Then for any $\vec{v}\ne \hat{y},\vec{v}\in W$, we have

$$||\vec{y}-\hat{y}||<||\vec{y}-\vec{v}||$$

Proof

$\vec{y}-\vec{v}=\vec{y}-\vec{v}+(\hat{y}-\hat{y})=(\hat{y}-\vec{y})+(\hat{y}-\vec{v})$ Pythagorean Theorem: $||\vec{y}-\vec{v}|{|}^2=||\hat{y}-\vec{y}|{|}^2+||\hat{y}-\vec{v}|{|}^2$ We know that $||\hat{y}-\vec{v}|{|}^2\ne 0$ as $\hat{y}\ne \vec{v}$, so $||\vec{y}-\vec{v}|{|}^2>||\vec{y}-\hat{y}|{|}^2$

---

Orthogonal Decomposition

Orthogonal Decomposition Theorem

Let $W$ be a subspace of ${\mathbb{R}}^n$. Then, each $\vec{y}\in {\mathbb{R}}^n$ has a unique decomposition.

$$\vec{y}=\hat{y}+z,\hat{y}\in W,z\in W^{\perp }$$

If $\overrightarrow{u_1},\dots ,\overrightarrow{u_n}$ is the orthogonal basis for $W$,

$$\hat{y}=\frac{\vec{y}\cdot \overrightarrow{u_1}}{\overrightarrow{u_1}\cdot \overrightarrow{u_1}}\overrightarrow{u_1}+\cdots +\frac{\vec{y}\cdot \overrightarrow{u_n}}{\overrightarrow{u_n}\cdot \overrightarrow{u_n}}\overrightarrow{u_n}$$

$\hat{y}$ is the orthogonal projection of $\vec{y}$ onto $W$