SVD

SVD

Suppose $A$ is an $m\times n$ matrix with singular values ${\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_n$ and $m\ge n$. Then $A$ has the decomposition $A=U\Sigma V^T$ where, \Sigma = \b{D\\0_{m-n,n}} \quad \quad D=\b{\sigma_1 &0 & \dots &0 \\ 0 & \sigma_2 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 &0&\dots & \sigma_n} $U$ is a $m\times m$ orthogonal matrix, and $V$ is a $n\times n$ orthogonal matrix. If $m<n$ then \Sigma= \b{D & 0_{m,n-m}}^T with everything else being the same.

Proof

Geometric Interpretation

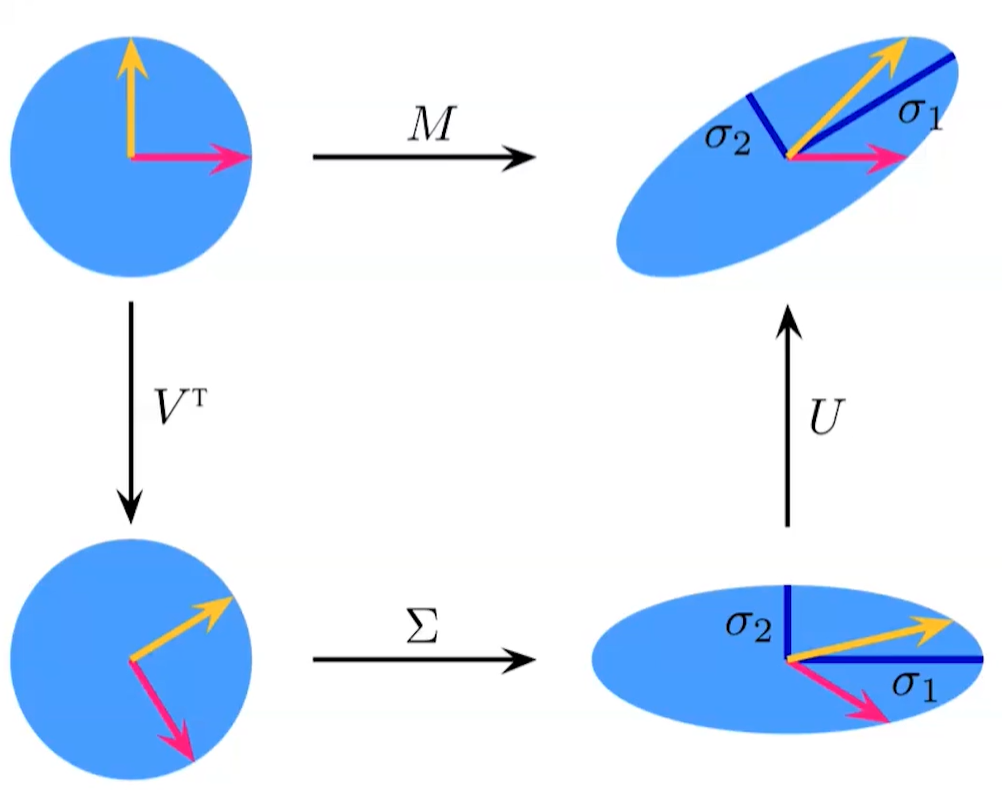
Computing

Suppose $A$ is $m\times n$ and has rank $r$.

1. Compute the squared singular values of $A^{T}A,{\sigma }_i^2$, and construct $\Sigma$.
2. Compute the unit singular vectors of $A^{T}A,{\vec{v}}_i$, use them to form $V$.
3. Compute an orthonormal basis for $\text{Col}A$ using, $\overrightarrow{u_i}=\frac{1}{{\sigma }_i}A\overrightarrow{v_i},i=1,2,\dots ,r$ If necessary, extend the set $\{\overrightarrow{u_i}\}$ to form an orthonormal basis for ${\mathbb{R}}^m$ and use the basis to form $U$.

Example

Find the SVD of A=\b{2&0\\0&-3\\0&0\\0&0}. A^TA=\b{4&0\\0&9}, \lambda_1=9, \lambda_2=4, \sigma_1=3 ,\sigma_2=2 So, \boxed{\Sigma = \b{3&0\\0&2\\0&0\\0&0}} Now find the right-singular vectors (i.e. eigenvectors of $A^{T}A$) for $V$, $$\begin{gathered} \overrightarrow{v_1}=\text{b}0 \\ 1\overrightarrow{v_2}=\text{b}1 \\ 0 \end{gathered}$$ Hence, \boxed{V=\b{0&1\\1&0}} Finally find $U$ using the left-singular vectors (i.e. orthonormal basis for $\text{Col}A$). This can be found by using $\frac{1}{{\sigma }_i}A\overrightarrow{v_i}$.

$$\begin{gathered} \begin{array}{rl}\overrightarrow{u_1}& =\text{b}0 \\ -1 \\ 0 \\ 0\\ \overrightarrow{u_2}& =\text{b}1 \\ 0 \\ 0 \\ 0\\ \overrightarrow{u_3}& =\text{b}0 \\ 0 \\ 1 \\ 0\\ \overrightarrow{u_4}& =\text{b}0 \\ 0 \\ 0 \\ 1\end{array} \end{gathered}$$

You may note that $\overrightarrow{u_3},\overrightarrow{u_4}$ are arbitrary, and this is true. They are any orthonormal vectors to $\overrightarrow{u_1},\overrightarrow{u_2}$ due to $\text{Rank}A=2$.

\boxed{ A= \b{0&1&0&0\\-1&0&0&0\\0&0&1&0\\0&0&0&1} \b{3&0\\0&2\\0&0\\0&0} \b{0&1\\1&0} }

Note: For finding $U\in {\mathbb{R}}^m$ if we have the vectors in $\text{Col}A$, and they are not enough to make an $m\times m$ matrix, then we will create any arbitrary vectors that are orthonormal to the vectors that you already have. Then we will run the Gram-Schmidt Process on these newly found vectors. All the vectors must be normalized at the end.

Properties of $V$ and $U$

For $i\le r=\text{Rank}A$

• $\overrightarrow{v_1},\dots ,\overrightarrow{v_r}$ is an orthonormal basis for $\text{Row}A$.
• $\overrightarrow{v_{r+1}},\dots ,\overrightarrow{v_n}$ is an orthonormal basis for $\text{Nul}A$.
• $\overrightarrow{u_1},\dots ,\overrightarrow{u_r}$ is an orthonormal basis for $\text{Col}A$.
• $\overrightarrow{u_{r+1}},\dots ,\overrightarrow{u_m}$ is an orthonormal basis for $\text{Nul}{A}^T$.