Least Squares

We want to find a line/curve that minimizes the sum of the square of the error caused due to deviation.

Least squares

The least squares for $Ax=b$ is $\hat{x}$ for which,

$$||b-A\hat{x}||\le ||b-Ax||$$

for all $x$

We can use the normal equation to solve for $\hat{x}$

Normal Equation

$$A^{T}A\hat{x}=A^T\vec{b}$$

Manipulating this we can get this,

$$\hat{x}=(A^{T}A{)}^{-1}{A}^T\vec{b}$$

Proof

Using QR Factorization

$$R\hat{x}=Q^T\vec{b}$$

Proof

$$\begin{array}{rl}{A}^{T}A\hat{x}& =A^T\vec{b}\\ (QR{)}^{T}QR\hat{x}& =(QR{)}^T\vec{b}\\ R^T{Q}^{T}QR\hat{x}& =R^T{Q}^T\vec{b}\\ R^{T}R\hat{x}& =R^T{Q}^T\vec{b}\\ R\hat{x}& =Q^T\vec{b}\end{array}$$

How to solve

Method 1

1. Construct QR Factorization
2. Solve $R\hat{x}=Q^T\vec{b}$

Method 2

1. Solve the normal equation for $\hat{x}$.

Method 3

1. Use Mean Deviation

Line

Say we want to find a line $y=mx+b$ that is the best fit for the following points:

x	-2	-1	1	1	2
y	-2	-1	1	2	2

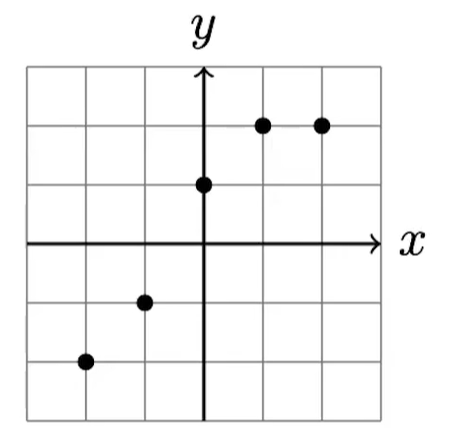We can create a list of linear equations using this:

$$\begin{array}{rl}m(-2)+b& =-2\\ m(-1)+b& =-1\\ m(1)+b& =1\\ m(1)+b& =2\\ m(2)+b& =2\end{array}$$

We can turn this in to a matrix equation like so, $A\vec{x}=\vec{b}$

$$\left[\begin{array}{cc}1& -2\\ 1& -1\\ 1& 1\\ 1& 1\\ 1& 2\end{array}\right]\left[\begin{array}{c}b\\ m\end{array}\right]=\left[\begin{array}{c}-2\\ -1\\ 1\\ 2\\ 2\end{array}\right]$$

Compute QR,

$$\left[\begin{array}{cc}\frac{1}{\sqrt{5}}& -\frac{2}{\sqrt{10}}\\ \frac{1}{\sqrt{5}}& -\frac{1}{\sqrt{10}}\\ \frac{1}{\sqrt{5}}& 0\\ \frac{1}{\sqrt{5}}& \frac{1}{\sqrt{10}}\\ \frac{1}{\sqrt{5}}& \frac{2}{\sqrt{10}}\end{array}\right]\left[\begin{array}{cc}\frac{5}{\sqrt{5}}& 0\\ 0& \frac{10}{\sqrt{10}}\end{array}\right]$$

Now compute $Q^T\vec{b}$, $Q^T\vec{b}=\left[\begin{array}{c}\frac{2}{\sqrt{5}}\\ \frac{11}{\sqrt{10}}\end{array}\right]$ Finally solve $R\hat{x}=Q^T\vec{b}$,

$$\left[\begin{array}{cc}\frac{5}{\sqrt{5}}& 0\\ 0& \frac{10}{\sqrt{10}}\end{array}\right]\hat{x}=\left[\begin{array}{c}\frac{2}{\sqrt{5}}\\ \frac{11}{\sqrt{10}}\end{array}\right]$$ $$\hat{x}=\boxed{\left[\begin{array}{c}\frac{2}{5}\\ \frac{11}{10}\end{array}\right]}$$

So we get $\boxed{y=\frac{2}{5}+\frac{11}{10}x}$

Curves

We can use this method to fit data to a curve using the function,

$$y=c_0+c_1{f}_1(x)+c_2{f}_2(x)+\cdots +c_n{f}_n(x)$$

Lets take an example, Say we want to modal:

x	-1	0	0	1
y	2	1	0	6

Using $y=c_{1}x+c_2{x}^2$

$$\begin{array}{rl}-c_1+c_2& =2\\ 0c_1+0c_2& =1\\ 0c_1+0c_2& =0\\ c_1+c_2& =6\end{array}$$

Now we can use one of the methods to solve for $c_1\text{ and }{c}_2$