Homogeneous Coordinates

Translations of points in ${\mathbb{R}}^n$ does not correspond directly to a linear transform. Homogeneous coordinates are used to model translations using matrix multiplication.

Homogeneous Coordinates in ${\mathbb{R}}^2$

Each point $(x,y)$ in ${\mathbb{R}}^2$ can be identified with the point $(x,y,H)$, $H\ne 0$, on the plane in $\mathbb{R}3$ that lies $H$ units above the $xy$-plane.

$(x,y)\to (x+h,y+k)$ can be represented by,

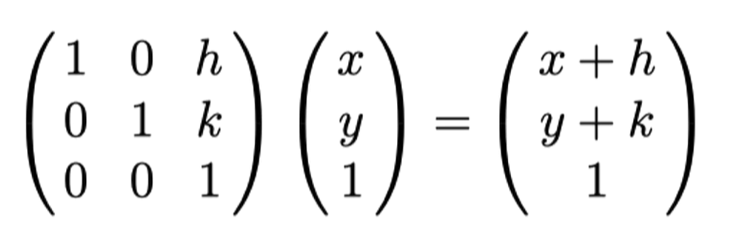
Now rotate a triangle ($(1,1),(2,4),(3,1)$) by $\frac{\pi }{2}$ radians counterclockwise about the point $(0,1)$.

$$\begin{array}{rl}d& =\left[\begin{array}{ccc}1& 2& 3\\ 1& 4& 1\\ 1& 1& 1\end{array}\right]\\ \text{Shift down by 1},& \\ \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& -1\\ 0& 0& 1\end{array}\right]d& =\left[\begin{array}{ccc}1& 2& 3\\ 0& 3& 0\\ 1& 1& 1\end{array}\right]\\ \text{Now rotate,}& \\ \left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& -1\\ 0& 0& 1\end{array}\right]d& =\left[\begin{array}{ccc}0& -3& 0\\ 1& 2& 3\\ 1& 1& 1\end{array}\right]\\ \text{Shift up by 1},& \\ \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 1\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}0& -3& 0\\ 1& 2& 3\\ 1& 1& 1\end{array}\right]& =\left[\begin{array}{ccc}0& -3& 0\\ 2& 3& 4\\ 1& 1& 1\end{array}\right]\end{array}$$

This give us the points, $(0,2),(-3,3),(0,4)$

In ${\mathbb{R}}^3$

So, $(x,y,z)\to (x+h,y+k,z+l)$ can be represented by,

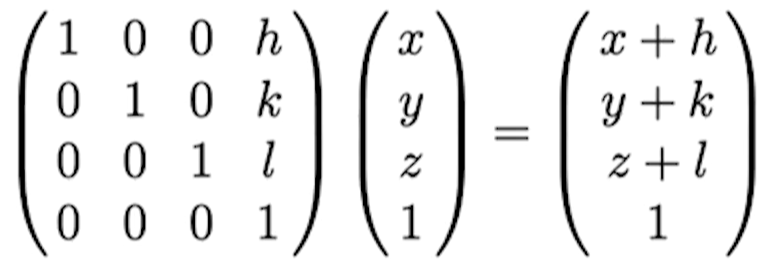
Rotation in ${\mathbb{R}}^3$

about $x_2$-axis by $\pi$ rads. To find $A=(a_1,a_2,a_3)$. We can find $T(e_1)$ as $T(e_1)=A{e}_1=a_1$. We can similarly find all the columns of $A$.

$$\begin{array}{rl}T(e_1)& =\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]\\ T(e_2)& =\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]\\ T(e_3)& =\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right]\\ A& =\left[\begin{array}{ccc}-1& 0& 0\\ 0& 1& 0\\ 0& 0& -1\end{array}\right]\end{array}$$

Projection

Onto the plane $x_3=4$ What should we do?

1. Shift everything down by 4 (Homogeneous Coordinates)
2. Apply the projection (Homogeneous Coordinates)
3. Shift everything back up by 4 (Homogeneous Coordinates) Amusing a vector $\vec{v}$,

$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 4\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& -4\\ 0& 0& 0& 1\end{array}\right]\vec{v}$$

You could drive the matrix but that is trivial and left as an exercise to the reader.

$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 4\\ 0& 0& 0& 1\end{array}\right]\vec{v}$$