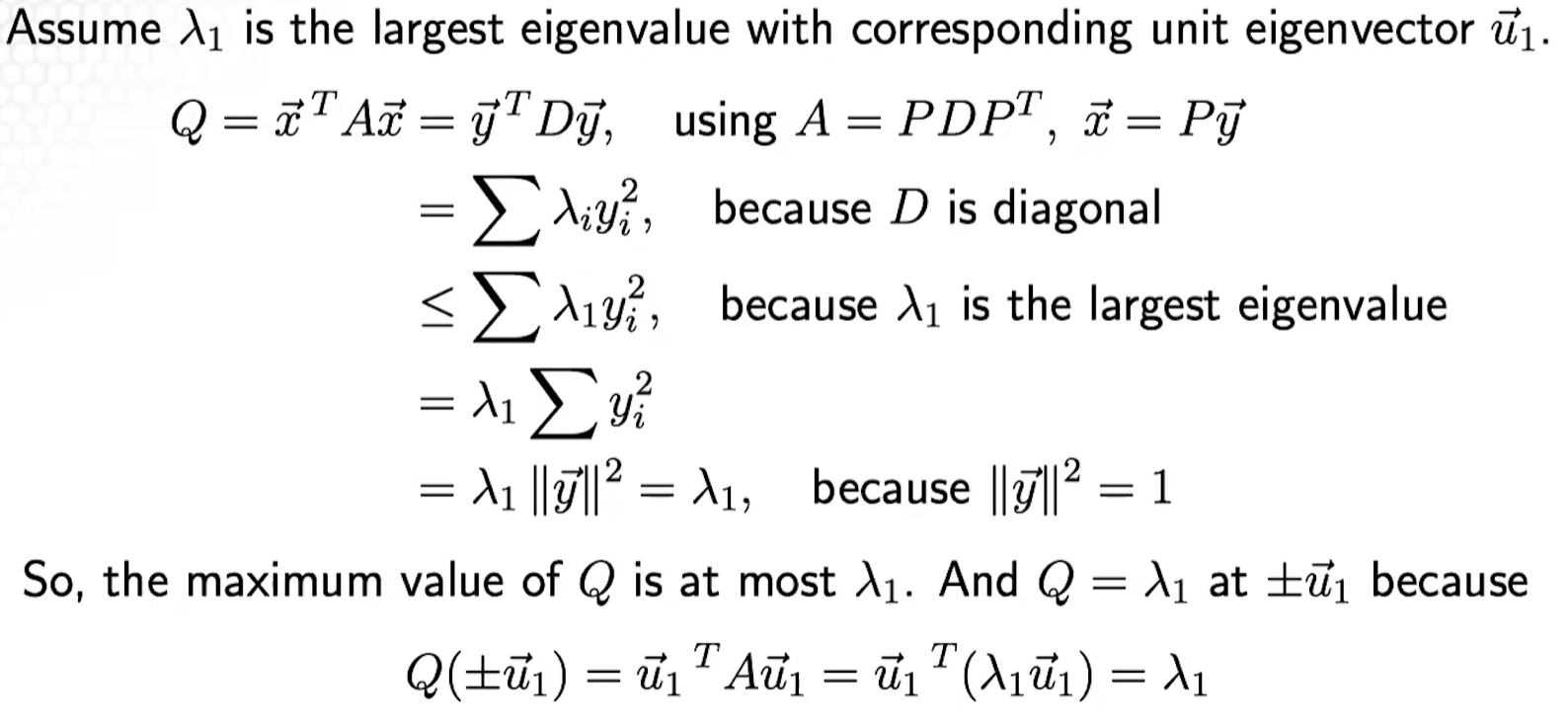Constrained Optimization

An example when $||x||=1$

We have a unit sphere $1=x_1^2+x_2^2+x_3^2=||x|{|}^2$. We wish to optimize $Q=9x_1^2+4x_2^2+3x_3^2$. To find the largest and smallest value of $Q$. It can be graphed as follows: 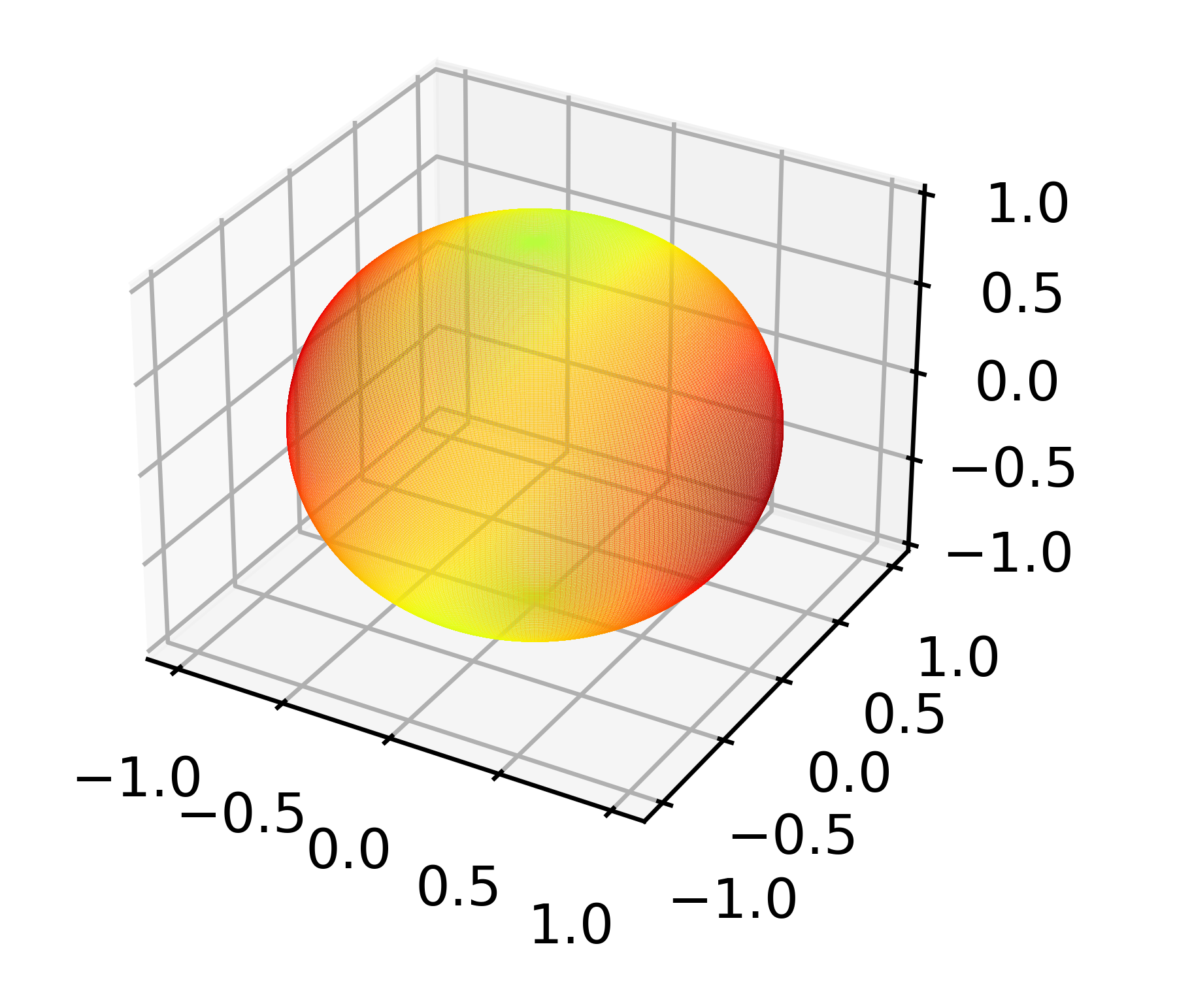We wish to maximize $Q$. $Q=9x_1^2+4x_2^2+3x_3^2={\vec{x}}^T\left[\begin{array}{ccc}9& 0& 0\\ 0& 4& 0\\ 0& 0& 3\end{array}\right]\vec{x}$ .

$$\begin{array}{rl}& \le 9x_1^2+9x_2^2+9x_3^2\\ & =9(x_1^2+x_2^2+x_3^2)\\ & =9||\vec{x}|{|}^2\\ & =9\end{array}$$

Note: $||\vec{x}|{|}^2=1$ because that is what we stated in the problem. So the max value of $Q$ is 1. More accurately, $\text{max}\{Q(\vec{c}):||\vec{x}||=1\}=9,$ and max occurs at $\vec{x}=\left[\begin{array}{c}\pm 1\\ 0\\ 0\end{array}\right]$. If we minimize $Q$, $\text{min}\{Q(\vec{c}):||\vec{x}||=1\}=3,$ and min occurs at $\vec{x}=\left[\begin{array}{c}0\\ 0\\ \pm 1\end{array}\right]$. Notice that the minimum and maximum values of $Q$ were the eigenvalues of $A$, and the corresponding normalized eigenvectors gave their locations.

Constrained Optimization

If $Q=x^{T}Ax$, $A$ is a real $n\times n$ symmetric matrix, with eigenvalues ${\lambda }_1\ge {\lambda }_2\cdots \ge {\lambda }_n$ and associated normalized eigenvectors $u_1,u_2,\dots ,u_n$ Also, $||x||=1$ Then max value of $Q(x)={\lambda }_1$ attained at $\pm u_1$ Then min value of $Q(x)={\lambda }_n$ attained at $\pm u_n$

Proof

Repeated Eigenvalue

If we have repeated eigenvalues then, the min and max values are found using the same prosses. The locations are the span of all the normalized eigenvectors of the corresponding min or max eigenvalue.