LU Factorization

Triangular Matrices

Upper Triangular

If $a_{i,j}=0$ for $i>j$ In other words the elements below the main diagonal are 0. Examples:

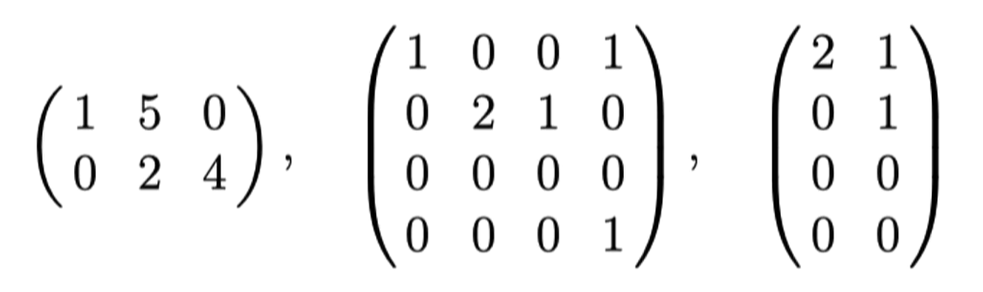
Lower Triangular

If $a_{i,j}=0$ for $i<j$ In other words the elements above the main diagonal are 0. Examples:

---

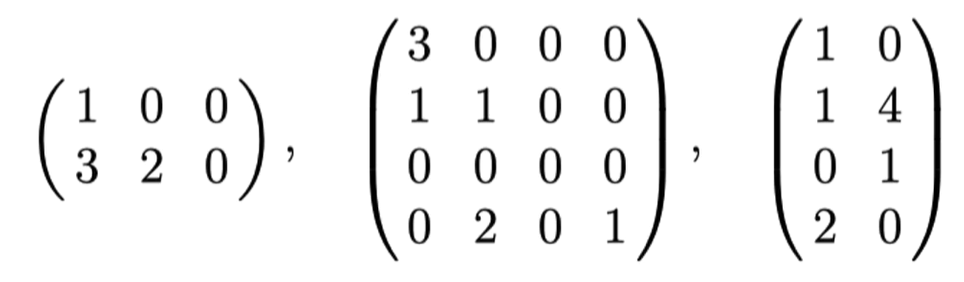
LU Factorization

If $A$ is an $m\times n$ matrix that can be row reduced to echelon form without row exchanges, then $A=LU$. $L$ is a lower triangular $m\times m$ matrix with 1’s on the diagonal, $U$ is an echelon form of $A$.

For example the $LU$ factorization of $A\in {\mathbb{R}}^{3\times 2}$ would look like:

$$A=LU=\left[\begin{array}{ccc}1& 0& 0\\ \ast & 1& 0\\ \ast & \ast & 1\end{array}\right]\left[\begin{array}{cc}\ast & \ast \\ 0& \ast \\ 0& 0\end{array}\right]$$

Algorithm

To solve $A\vec{x}=\vec{b}$ for $\vec{x}$:

1. Construct the $LU$ decomposition of $A$ to obtain $L$ and $U$.
2. Set $U\vec{x}=\vec{y}$. Forward solve for $\vec{x}$ in $L\vec{y}=\vec{b}$.
3. Backwards solve for $\vec{x}$ in $U\vec{x}=\vec{y}$.

In other words: Get LU Then solve $L\vec{y}=\vec{b}$ for $\vec{y}$ Finally use that $\vec{y}$ to solve for $\vec{x}$ in $U\vec{x}=\vec{y}$

Computing LU

You are not allowed to swap rows. Also Scalar Multiplication is not needed. $E_p\cdots E_{1}A=U$ $E_j$ are matrices that perform elementary row operations. Because we did not swap rows, each $E_j$ happens to be lower triangular and invertible

$$\begin{array}{c}\begin{array}{rl}{E}_p\cdots E_{1}A& =U\\ L{E}_p\cdots E_{1}A& =LU\\ L{L}^{-1}A& =LU\\ A& =LU\end{array}\end{array}$$

$\boxed{E_p\cdots E_1=L^{-1}}$ To compute the $LU$ decomposition:

1. Reduce $A$ to an echelon form $U$ by a sequence of row replacement operations, if possible.
2. Place entries in $L$ such that the same sequence of row operations reduces $L$ to $I$.

Example

Compute the $LU$ factorization of:

$$A=\left[\begin{array}{cccc}4& -3& -1& 5\\ -16& 12& 2& -17\\ 8& -6& -12& 22\end{array}\right]$$

Reducing it to echelon form we get:

$$U=\left[\begin{array}{cccc}4& -3& -1& 5\\ 0& 0& -2& 3\\ 0& 0& 0& -3\end{array}\right]$$

To reduce it we use the following row operations:

$$\begin{array}{c}\begin{array}{rl}{R}_2& +4R_1\\ R_3& -2R_1\\ R_3& -5R_2\end{array}\end{array}$$

So $L$ will be such that the same sequence of row operations reduces $L$ to $I$.

$$L=\left[\begin{array}{ccc}1& 0& 0\\ -4& 1& 0\\ 2& 5& 1\end{array}\right]$$